This month we are working on classifying quadrilaterals. Creating these overlapping hierarchies is always a challenge. Relationships that work one way, don’t work the other way, and there is a lot of specific vocabulary that needs to be learned and applied in novel situations.
It’s a little like this: everyone who lives in Olympia lives in Washington, but not everyone who lives in Washington lives in Olympia. Bringing it back to the shapes – all squares are rectangles, but not all rectangles are squares.
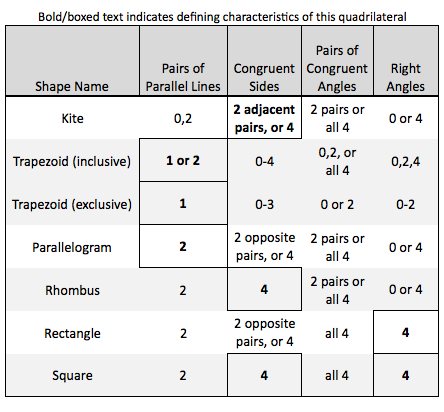
To do this work, we need to know the defining characteristics of the quadrilaterals that we are classifying – and here we run into yet another difficulty… mathematicians don’t always agree on these! But the work of classification goes on. We just learn the specific characteristics and create the relationships accordingly. Here is a table that tries to communicate these overlapping relationships.
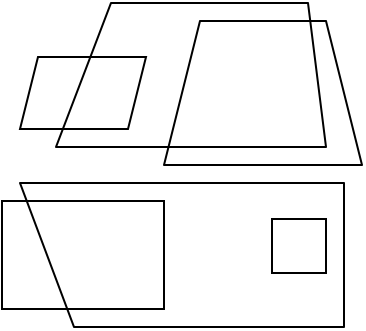
Under the inclusive definition of trapezoids, all six shapes a the top of this post are trapezoids, under the exclusive definition only three of them are… can you spot them?
From Howard Phillips
From early years kids naturally like exclusive definitions, and have to be weaned off this. This would be easier if we were more careful with the word “is”. Even to me the statement ” a square is a rhombus” sounds weird, if not actually wrong. It would be better to be less brutal, and say “a square is also a rhombus” (and all the other such statements).
Even better, and quite mathematical, is the phrasing “a square is a special case of a rhombus”, as the idea of special cases is very important, and usually overlooked.
It is odd that the classification of triangles is done entirely with adjectives and the difficulty is thus avoided.
There’s the added complication that trapezoids are trapeziums in the UK!
The last couple of years I’ve chosen to look at the properties of hexagons instead. The snow is fresher. There’s not a long tradition of naming to catch up with, so the students can be involved in the categorisation more actively.
I’ve been helped a lot in this by Christopher Danielson’s two-minute video on using hexagons:
http://www.mathagogy.com/christopher-danielson-how-i-teach-proof/
I found it difficult to find the “exclusive” trapezoids/trapeziums. I think that this is because I had my own understanding firmly entrenched so that I rejected the new learning. I know that this is often how students approach their learning also: rejecting new information when it doesn’t sit well with what they already know (or think they know). This is why I think it is important for math teachers to keep learning, to keep absorbing new knowledge: it helps us to relate to kids when they are in a state of confusion.