Three people are offered an opportunity. They will be brought at random and one at a time into a room that contains a simple light switch and a working light. Any of the three may be brought into this room multiple times, even multiple times in succession. If any one of the three is able at any time to correctly deduce that all three of them have been brought into this room, they will win 1 million dollars. If the deduction is incorrect, they will each have to pay $10,000. If they are allowed to meet and confer together before the random procedure begins, what plan will ensure they win the money and not run the risk of having to pay? Assume that the light is on at the beginning and that only the three people are allowed to flip the light switch.
A Year in Reflection
As this year comes to a close, I want to tell you, my fellow bloggers and all of those who have left responses, how much you have inspired my teaching and growth throughout this year. When I think back to the beginning of the year and our discussion of starting this blog, I think about how vital it was for all of us as teachers to foster a Growth Mindset in our students. Now that the year is winding down, I am curious about how you feel with regards to Growth Mindset in your students.
On the first day of school, I asked my students the following questions:
- How do you feel when you make a mistake in math?
- What would you like me to say when you make a mistake?
- What would you like to classmates to say when you make a mistake?
- How do you think we can best support each other in this class, especially when someone makes a mistake?
Responses to these questions were eye-opening and varied greatly. Some students wrote comments from: mistakes turn “into an opportunity to learn better,” and “mistakes help me grow,” to mistakes make me feel “angry,” “like I am going to cry,” and “frustrated/annoyed.” As I reflect on the students who had a negative self concept when making mistakes, I am curious about how their feelings have changed since the beginning of the year, if at all.
This week, I plan to give students back their written responses from the first day of school and answer these questions again. In my observations, we have come SO far as a learning community, and I can’t wait to hear how my students respond now (I will definitely share in a future post).
I am curious about what you are all doing with regards to end of year reflections, how you feel about your progress with Growth Mindset, and what this makes you think about for next year.
Do We Really Have a Problem Here?
As a teacher, I usually favor spending money on public schools. Our teachers union voted to walk out this coming Tuesday afternoon to ask for more money for our kids. After the vote, however, I wondered how bad our situation really was. Compared to other states around the country, do we really have a school funding problem? I found some numbers and after a bit of analysis decided to pose the same question to my sixth graders.
One up-to-date and reliable data set that I thought would matter and be accessible to middle school students was per pupil expenditures by state. I found it at the Kids Count Data Center. It made sense to use these numbers because a data set of fifty is manageable and the sixth grade learning sequence demands understanding of distributions, box plots and quartiles. The class was in its third day of a statistics unit.
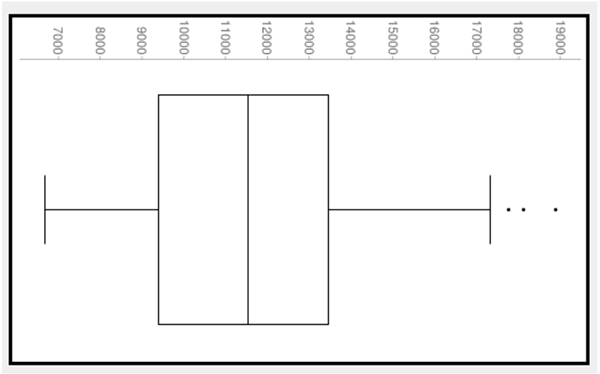
I proposed to the class that they would be using statistics to decide for themselves whether or not they agreed that their teachers should walk out to demand more money for schools. I passed out forty-nine numbers on index cards: one number for each state. I held our state of Washington face down in my hand. I told them that they were holding one, two or three states in their hands and that the numbers were in thousands. I didn’t write the names of the states on the cards so that the curious could ask about the states they held. One lay way outside the bulk of the numbers, drawing envy and attention to the state of Vermont which spends close to $19,000 per year per student. The class quickly determined that Utah had the lowest spending at a little under $7,000 per year per student.
I showed the five number summary I had calculated in advance:
- Minimum: 7
- Maximum: 19
- Median (or middle:) 10.5
- 1st Quartile (middle of the bottom half:) 9
- 3rd Quartile (middle of the top half:) 13.5
I stood in the middle of a line on the floor and proclaimed myself the median (the middle number when numbers are arranged in order,) and asked everyone who had a card below the median (in the bottom half) to place it on the floor. Then those between the median (middle) and third quartile (the top fourth) of the states came forward to place their cards. Finally, I stood at the third quartile and asked the big spenders (the top fourth of the states) to come forward.
Then I stepped out of the line and asked if anyone had any questions. Hands shot up as several students blurted, “Where is Washington?” I said, “I am still holding that card. Where do you think we belong in this distribution?” A few pointed to the minimum, assuming that we keep company with Utah, but most pointed to near the middle of the line.
I stepped forward with my card with the nine on it and stood at the first quartile which marks the top of the bottom fourth of state spending. I asked students what that meant. They replied with dismay, “Three-fourths of the states spend more on kids than we do.” Then I stepped out of the line again and took my place just eight states from the bottom. I said, “Yes you are right, and with a total of about six states spending around $9,000 per student, we are about eight states from the bottom. Do we have a problem? Talk to your partner about whether we have a problem.”
I didn’t ask students to write down their replies because I want them to be free to decide for themselves if Washington State has a school funding problem. I decided that asking them to share would put them too much on the spot. The pressure of writing something down didn’t feel right: It is my job to provide information, not to persuade.
When they shared out, most agreed that we have a problem. One pair dissented and wisely said, “We think we need more information. It depends what they spend the money on, like tests or teachers or field trips or sports.” I told them that another data set I could have brought was teacher salaries. “I am fine,” I said, “but a beginning teacher makes the same hourly wage as my eighteen year old son does building trails in the state forest.” Another student made the argument that his grandma was a teacher and things must be fine because she has good retirement, but then he caught himself, “Wait, she lives in Vermont.”
I agree with the pair of student skeptics. We do need more information. How districts spend the money does matter. But without the money to spend, those closest to the students — the principals and the teachers — won’t even have the option to choose to spend wisely. I don’t plan on moving to Vermont, but I do know my talented student teacher is leaving the state for Oregon, where spending is near the median.
I don’t know how many families will join us on Tuesday, but the parent volunteer in the room was swayed by the data to reach out via email to the families of my class. For those willing, let’s meet at Percival Landing at noon, Tuesday, May 26, all dressed in red and walk to the Capital Building for our kids!
Why Not Helping is Helping
I have taught math in public schools for thirteen years. Each new batch of students comes with a handful of parents who grapple with how best to help their children wrestle with math homework. You, yourself, may be one of those parents. When faced with math tasks asking for explanation of reasoning, or when the new-fangled curriculum wields a new strategy in place of familiar algorithms, the kettle of parents minds starts to bubble, roil, and whistle.
Dear Parents,
I have good news, a simple mandate which will both alleviate this internal pressure to perform math miracles AND will be better for your child’s math. The advice? BE LESS HELPFUL.
Don’t answer their questions. Don’t show them shortcuts. Above all, DO NOT teach them the old tried and true shortcuts of the standard algorithm.
I am not giving you a free pass, here. Notice, I did not say, “Make them do their math all by themselves.” Rather, I want you to enter their world of confusion with them. Pull up a chair. Grab some scratch paper. Do the problem with them. Not for them. With them. Answer their question with more questions. Verbalize when you get stuck. Normalize the struggle.
One common deficit in our students is their inability or unwillingness to ask questions. But if a student can verbalize what they don’t understand, if they can formulate a question, then they are in an infinitely better place than if they quit before really diving head-long into the pool of problems. Your best way of helping them is to role model these skills. Make them teach you.
When you get stuck on a math problem, don’t give up. Persist. If you have no idea how to do a problem, guess. Make an assumption and run with it. If that assumption helps you solve the problem, hallelujah! If not, even better. Now you can go back to the assumption and say, “Now I know that this is wrong! Therefore, it must mean blah blah blah instead!” Then off you go, down another rabbit hole of problem solving.
Another deficit in our math students is learned helplessness. Many are unwilling to even try. Show them how to make mistakes. Gracefully! With aplomb! With pride! What’s more, celebrate those moments, for this is where true learning lies. Do a happy dance! Pump your fists! Cheer!
Now, if on a particular problem, you have reached the dead-end of this logical alleyway, you and your student are in the prime position to express what you don’t understand. Have your kid write down this question in place of an answer. Have them staple together all their failed attempts to turn in. If your math teacher is worth their mustard, they will honor this work and highly appreciate it. This makes their job far easier: they no longer have to guess why their kids aren’t getting this.
In conclusion, I would like to say thank you. Thank you for being involved in your children’s education. If you are reading this blog, then you are truly exceptional in your level of commitment to their education. You already know that helping kids with their academics is difficult. It is a problem. It is your homework problem. Math is the process of identifying problems, then methodically going about solving them. This is the perfect opportunity to practice what I’m preaching.
So don’t look for short cuts. Don’t look for easy fixes. Look for a solution. And this part is probably self obvious (but for some reason, not always in math): don’t give up; persist; the solution is out there somewhere, sitting right next to your kid.
Pattern and Order
My principal came up to me the other day and told me that he just had one of the strangest conversations he’s ever had in education. A few girls from my class had just excitedly shared with him that they were on fire with math. He’s more of a language arts enthusiast, and I guess he had never seen the glow from anyone who has just glimpsed some underlying order, just uncovered something mystical, something deep and hidden in numbers. It’s pretty awesome when that happens. Our class, and these girls in particular have been having a really good time discovering these patterns. First in the sequences of tiles or blocks, then through the distances between the numbers and the rates of change, and finally on the coordinate plane. It’s a wonderful thing to connect a physical model, the ordered pairs that describe it, and a graph – it’s practically poetry.
Below is the “pool” sequence. The gray tiles are the border and the white tiles are the surface area of the water in the pool.
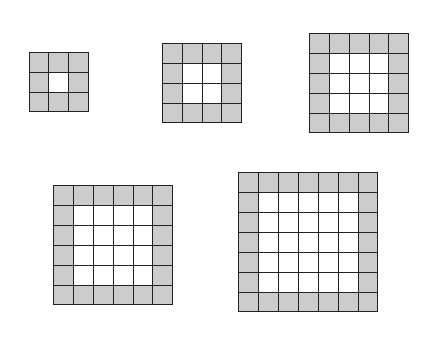 This was one of the first sequences we looked at. Not the first mind you, but it surprised me how soon we got into functions that were non-linear. Actually, this non-linear function was easier for the kids to decode than the linear one that accompanied it. First students shared their observations:
This was one of the first sequences we looked at. Not the first mind you, but it surprised me how soon we got into functions that were non-linear. Actually, this non-linear function was easier for the kids to decode than the linear one that accompanied it. First students shared their observations:
- The water gets bigger by 3 (the first time)
- Next it goes up by 5
- Pool area goes up by increasing odd numbers (+1, +3, +5…)
- Pool area is 1×1, 2×2, 3×3…
- Odd arrangements have a center tile
- Sides of the pool get bigger by 1
- Arrangement number is 2 less than side length
- Pool and border expand at different constant [sic] rates
- Arrangement 1 fits into the “white” of arrangement 3
- It looks like arrangement 3 fits into 5’s pool
- All odd arrangements fit into next odd ‘s white
Next we looked at the patterns that happen in the numbers. Below is a table of arrangement numbers (x), the number of border tiles (y), and some other observations.
| Arrangement (x) | Pool Border (y) | Observations | Rule? |
|---|---|---|---|
| 1 | 8 | 5x + 3 | |
| 2 | 12 | +4 | 5x + 2 |
| 3 | 16 | +4 | 5x + 1 |
| 4 | 20 | +4 | 5x + 0 |
| 5 | 24 | +4 | 5x - 1 |
One student got really excited to see her pattern continue indefinitely. We looked back at the tile models to see how we could “see” the growth by 4 that shows up in the table. This yielded some really neat connections (and I think we came to a more formal rule). Next came the data for the water tiles. This one was snatched up easily, but the significance of our departure from linear relationships was not clear until we examined the graph.
| Arrangement (x) | Pool Area (y) | Observations | Rule? |
|---|---|---|---|
| 1 | 1 | x * x | |
| 2 | 4 | +3 | x * x |
| 3 | 9 | +5 | x * x |
| 4 | 16 | +7 | x * x |
| 5 | 25 | +9 | x * x |
Up until now, students had been seeing even steps – constant rates of change. Our outputs had always gone up by the same amount in each iteration of the sequence. With the pool area, each subsequent arrangement was significantly larger than the previous. The steps (up the y-axis) were getting increasingly tall.
The green line is the graph of the border and the red line is the graph of the pool area.
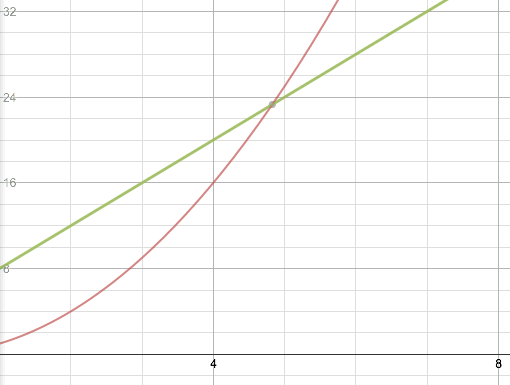 After putting all of this together, students were able to make predictions about how many tiles would be in some distant arrangement, and even find out which arrangement would have a certain number of tiles. Try it out for yourself!
After putting all of this together, students were able to make predictions about how many tiles would be in some distant arrangement, and even find out which arrangement would have a certain number of tiles. Try it out for yourself!
1. How many border tiles will be in any arrangement? How many pool tiles will be in any arrangement?
2. Which arrangement will have 196 tiles total for both border and pool?*
*I can’t say if my 5th graders solved this one yet… we’ll have to come back to this after spring break.