This month we are working on classifying quadrilaterals. Creating these overlapping hierarchies is  always a challenge. Relationships that work one way, don’t work the other way, and there is a lot of specific vocabulary that needs to be learned and applied in novel situations.

It’s a little like this: everyone who lives in Olympia lives in Washington, but not everyone who lives in Washington lives in Olympia. Bringing it back to the shapes – all squares are rectangles, but not all rectangles are squares.

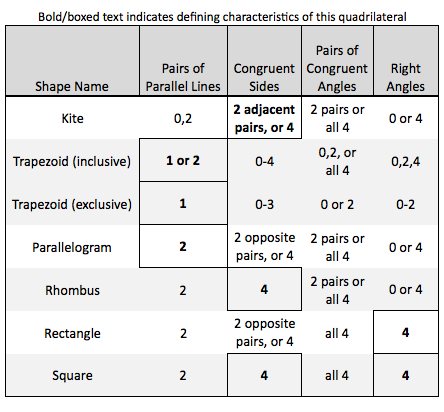
To do this work, we need to know the defining characteristics of the quadrilaterals that we are classifying – and here we run into yet another difficulty… mathematicians don’t always agree on these! But the work of classification goes on. We just learn the specific characteristics and create the relationships accordingly. Here is a table that tries to communicate these overlapping relationships.

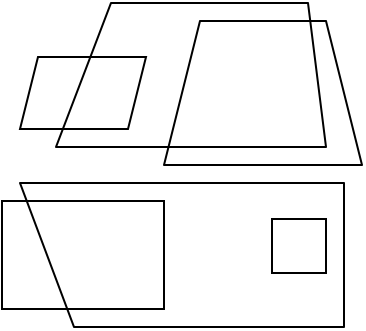
Under the inclusive definition of trapezoids, all six shapes a the top of this post are trapezoids, under the exclusive definition only three of them are… can you spot them?