Monthly Archives: March 2015

Arithmetic, Math Fluency, Thoughts on Learning

Ours is to Wonder Why

Leave a comment

It began almost accidentally. After fooling around with some interesting magic squares recently I decided to put a couple in front of my students. I wanted to step away from our work with division of fractions momentarily and ignite their curiosities. Below is the fist magic square I showed them.

ms1I won’t bore you by telling you about all of the amazing patterns inside this square – they are yours to discover. In class we shared things we noticed. One of my students noted something like “It goes 8 – 5 – 2 diagonally: each number three less than the one before?” (Notice the question mark?) I said “Are you asking me? You’ve got to make a statement! You’ve made a discovery! You’ve got to stand up and shout EUREKA! So from here on out the class made really exciting discoveries punctuated by shouts of “Eureka!”

Then we looked at the following magic square.

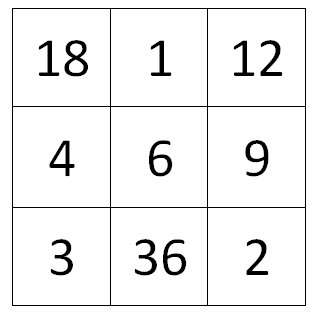ms2What do you notice? We made one discovery after another – the class was reaching a fevered pitch: math was rocking the house, and the students’ excitement and engagement was running into the red. Time to change gears and use some of this fuel on division of fractions.

Division of fractions – something like 2/3 ÷ 1/4 – is an odd thing to get your head around. We’ve been working with visual models for a little while but it still takes some mental work to see this stuff. In the old days there used to be this saying in elementary math about dividing fractions: “Ours is not to wonder why, just invert and multiply.” Catchy, but this takes all of the understanding right out of the equation (math joke!). Maybe the problem looks like this:

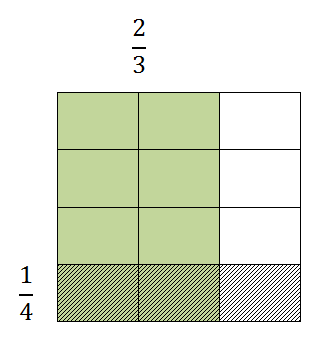grid1Here we see a rectangle that is cut into thirds vertically and fourths horizontally. Each column represents one-third and each row is one-fourth. So the question is: How many of the shaded areas will fit into the green area? If we rotate the one-fourth, we can fit two full fourths into the green area (below). In the remaining green area we can only fit 2/3 of a quarter strip.

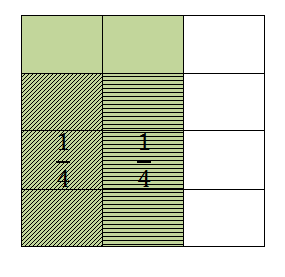grid-div2So the number of fourths that can fit is 2 and 2/3. You can think about it this way: How many groups of 1/4 can I make with 2/3 of a whole? Scoop, scoop, little scoop.

If we look at the equations we can make some sense of these as well. Notice that in the equation below, we just combine the fractions into one fraction and the result is another way of looking at the picture above! How many 3/4 can fit into 2 wholes? – except this time the whole is actually just one-quarter! Do you see it?

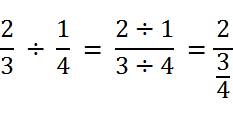eq1Maybe you don’t like that one… OK, I can live with that. But what if we did something interesting like found a common denominator for the fractions. 2/3 = 8/12 and 1/4 = 3/12.

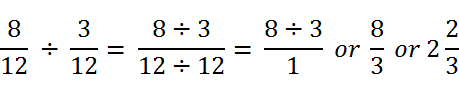eq2In this equation, the quotient of the first expression gives us 1 in the denominator! So it effectively becomes 8 ÷ 3 or 8/3, which is 2 and 2/3. This technique just melts the fraction division away.

All of this happened in one class. And there were more problems than just this one and more voices than just mine. Students were explaining what they saw and why it made sense, and they were shouting “Eureka!” every time they understood something new. Many students were standing, and hands were waving all around the room. I can tell you that at times it got a little crazy. But this is how, at 12:20pm, after a long morning of classes culminating in a math lesson on the division of fractions, a group of 25 fifth-graders spontaneously erupted into applause. It certainly doesn’t happen every day.

Ours is definitely to wonder why.

Thoughts on Learning

My Fear of Math Phobias

8 Comments

!

There is one idea that I would love to disappear completely from math discussions: “math phobia.” Vamoose! Vanish! Evanesco! Of all the ideas that are harmful or destructive to students’ acquisition of math ideas, “math phobia” is one of the worst.

Yet, I hear it all the time. I hear it from adults all the time. I hear it from parents. What is worst of all is that I hear it from other teachers. “I am not good at math”; “I never did understand that”; “go ask your dad”; and the darndest of them all: “I hate math.” To beat all, they say it right in front of kids–their own kids and students.  Sometimes, I’m not sure if they are calling themselves or the math itself stupid.

Now, I am not saying that there is no such thing as math phobia. I am sure that some people actually run in fear when they see numbers on street signs. I am certain that somewhere, men and women are cowering, shivering in their closets because they read “¼ cup of sugar” in a recipe, or a telephone number flashed up on the screen when they were watching the television.

What I am saying, though, is that these phrases and attitudes give kids a free pass. They hear the adults walking around dismissing their own mental power all the time. So they do it, too. Kids become lethargic. Kids start saying, jokingly at first, that they aren’t good at math. But by the fifth grade, I see many kids completely checked out. It’s not that they couldn’t understand the math problems. They simply have become so used to not putting in the required brain power (which is not that much voltage, incidentally).

So parents, I implore you: zip those math-phobic lips! Pretend that you love math DESPITE all the damaging math classes you had as a youth. Refuse to pass the buck to your partner who “has the math smarts in the family.”  Instead, each time you notice the beauty in a flower or the symmetry in a piece of artwork, declare, “Ah! Look at the geometry on that puppy!”

This may drastically change the way you interact with your students around math and around homework. Instead of the instructional coach, you are now fellow math adventurer. Talk less about how to do the math and more about what it makes you think of. Where do you see the patterns in the real world? Where does geometry show up in art and architecture? Where do fractals sprout up in the coral reefs and forests?

One more thing, don’t be afraid of pointing out short cuts. If your kid is spending much extra time and effort on a problem which has a more direct and elegant solution, go ahead and say, “Son, have you ever thought of [blah blah blah]?” Or, “Daughter of mine, I see that you are stumped here, but maybe you could solve an easier problem.”  What this will roll model is that mathematicians aren’t into punishing themselves. We are all about making work easier; making the world around us easier to understand. What is so scary about that?

Thoughts on Learning

Bridge to Multi-Digit Subtraction Standard Algorithm

4 Comments

In my 12th year of teaching, I continue to be amazed at the misconceptions surrounding multi-digit subtraction. In my experience, students who are masters at memorizing the steps of the US standard algorithm are quite successful, though have little understanding of the place value. Why do we borrow? What does that even mean?

In an effort to do a much better job this year, I am trying a new strategy. Given the problem:

634 – 368 = z

I am requiring my students to write out each number in expanded form:

634 = 600 + 30 + 4

368 = 300 + 60 + 8

The language that I am using with this strategy is intentional. Since we cannot take 8 from 4, we need to borrow a ten, thus changing the 30 to a 20 and changing the 4 to a 14. I am stressing with students that this is the same value:

600 + 30 + 4 = 600 + 20 + 14

This alone is mind-blowing!

So now, if we finish the problem, it looks like:

subtract

The power in this language is that now, rather than saying: “What is 12 – 6? ” I am now saying, “What is 120-60?” My hope is that by changing the way I speak, I am deepening students’ understanding of place value, and how we talk about it. The best part of this is that when I revert to my old ways (which I do), students immediately correct me by saying,  “Excuse me, Mrs. Nied, but that is not 12-6–it is 120-60.”  Students have completely taken over this language and I am hearing it constantly in group discussions. Woo hoo!