Three people are offered an opportunity. They will be brought at random and one at a time into a room that contains a simple light switch and a working light. Any of the three may be brought into this room multiple times, even multiple times in succession. If any one of the three is able at any time to correctly deduce that all three of them have been brought into this room, they will win 1 million dollars. If the deduction is incorrect, they will each have to pay $10,000. If they are allowed to meet and confer together before the random procedure begins, what plan will ensure they win the money and not run the risk of having to pay? Assume that the light is on at the beginning and that only the three people are allowed to flip the light switch.
All posts by Spencer Olmsted
Pattern and Order
My principal came up to me the other day and told me that he just had one of the strangest conversations he’s ever had in education. A few girls from my class had just excitedly shared with him that they were on fire with math. He’s more of a language arts enthusiast, and I guess he had never seen the glow from anyone who has just glimpsed some underlying order, just uncovered something mystical, something deep and hidden in numbers. It’s pretty awesome when that happens. Our class, and these girls in particular have been having a really good time discovering these patterns. First in the sequences of tiles or blocks, then through the distances between the numbers and the rates of change, and finally on the coordinate plane. It’s a wonderful thing to connect a physical model, the ordered pairs that describe it, and a graph – it’s practically poetry.
Below is the “pool” sequence. The gray tiles are the border and the white tiles are the surface area of the water in the pool.
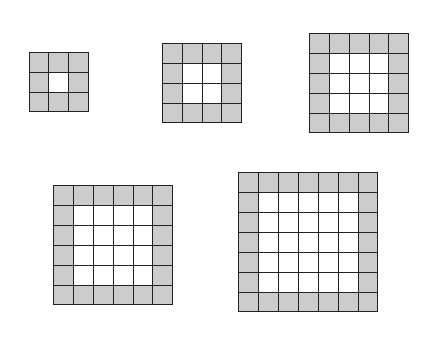This was one of the first sequences we looked at. Not the first mind you, but it surprised me how soon we got into functions that were non-linear. Actually, this non-linear function was easier for the kids to decode than the linear one that accompanied it. First students shared their observations:
- The water gets bigger by 3 (the first time)
- Next it goes up by 5
- Pool area goes up by increasing odd numbers (+1, +3, +5…)
- Pool area is 1×1, 2×2, 3×3…
- Odd arrangements have a center tile
- Sides of the pool get bigger by 1
- Arrangement number is 2 less than side length
- Pool and border expand at different constant [sic] rates
- Arrangement 1 fits into the “white” of arrangement 3
- It looks like arrangement 3 fits into 5’s pool
- All odd arrangements fit into next odd ‘s white
Next we looked at the patterns that happen in the numbers. Below is a table of arrangement numbers (x), the number of border tiles (y), and some other observations.
| Arrangement (x) | Pool Border (y) | Observations | Rule? |
|---|---|---|---|
| 1 | 8 | 5x + 3 | |
| 2 | 12 | +4 | 5x + 2 |
| 3 | 16 | +4 | 5x + 1 |
| 4 | 20 | +4 | 5x + 0 |
| 5 | 24 | +4 | 5x - 1 |
One student got really excited to see her pattern continue indefinitely. We looked back at the tile models to see how we could “see” the growth by 4 that shows up in the table. This yielded some really neat connections (and I think we came to a more formal rule). Next came the data for the water tiles. This one was snatched up easily, but the significance of our departure from linear relationships was not clear until we examined the graph.
| Arrangement (x) | Pool Area (y) | Observations | Rule? |
|---|---|---|---|
| 1 | 1 | x * x | |
| 2 | 4 | +3 | x * x |
| 3 | 9 | +5 | x * x |
| 4 | 16 | +7 | x * x |
| 5 | 25 | +9 | x * x |
Up until now, students had been seeing even steps – constant rates of change. Our outputs had always gone up by the same amount in each iteration of the sequence. With the pool area, each subsequent arrangement was significantly larger than the previous. The steps (up the y-axis) were getting increasingly tall.
The green line is the graph of the border and the red line is the graph of the pool area.
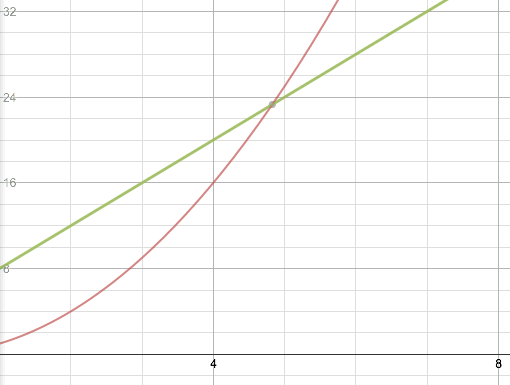After putting all of this together, students were able to make predictions about how many tiles would be in some distant arrangement, and even find out which arrangement would have a certain number of tiles. Try it out for yourself!
1. How many border tiles will be in any arrangement? How many pool tiles will be in any arrangement?
2. Which arrangement will have 196 tiles total for both border and pool?*
*I can’t say if my 5th graders solved this one yet… we’ll have to come back to this after spring break.
Ours is to Wonder Why
It began almost accidentally. After fooling around with some interesting magic squares recently I decided to put a couple in front of my students. I wanted to step away from our work with division of fractions momentarily and ignite their curiosities. Below is the fist magic square I showed them.
I won’t bore you by telling you about all of the amazing patterns inside this square – they are yours to discover. In class we shared things we noticed. One of my students noted something like “It goes 8 – 5 – 2 diagonally: each number three less than the one before?” (Notice the question mark?) I said “Are you asking me? You’ve got to make a statement! You’ve made a discovery! You’ve got to stand up and shout EUREKA! So from here on out the class made really exciting discoveries punctuated by shouts of “Eureka!”
Then we looked at the following magic square.
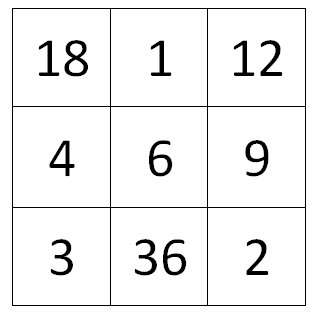What do you notice? We made one discovery after another – the class was reaching a fevered pitch: math was rocking the house, and the students’ excitement and engagement was running into the red. Time to change gears and use some of this fuel on division of fractions.
Division of fractions – something like 2/3 ÷ 1/4 – is an odd thing to get your head around. We’ve been working with visual models for a little while but it still takes some mental work to see this stuff. In the old days there used to be this saying in elementary math about dividing fractions: “Ours is not to wonder why, just invert and multiply.” Catchy, but this takes all of the understanding right out of the equation (math joke!). Maybe the problem looks like this:
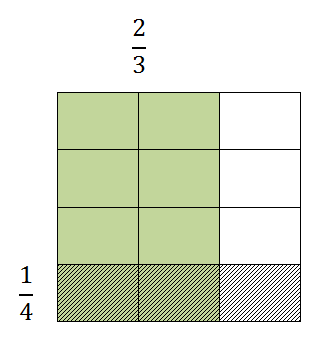Here we see a rectangle that is cut into thirds vertically and fourths horizontally. Each column represents one-third and each row is one-fourth. So the question is: How many of the shaded areas will fit into the green area? If we rotate the one-fourth, we can fit two full fourths into the green area (below). In the remaining green area we can only fit 2/3 of a quarter strip.
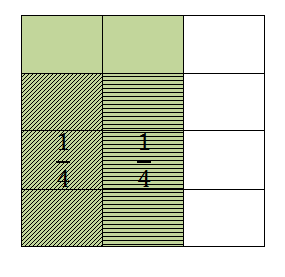So the number of fourths that can fit is 2 and 2/3. You can think about it this way: How many groups of 1/4 can I make with 2/3 of a whole? Scoop, scoop, little scoop.
If we look at the equations we can make some sense of these as well. Notice that in the equation below, we just combine the fractions into one fraction and the result is another way of looking at the picture above! How many 3/4 can fit into 2 wholes? – except this time the whole is actually just one-quarter! Do you see it?
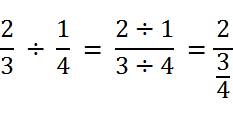Maybe you don’t like that one… OK, I can live with that. But what if we did something interesting like found a common denominator for the fractions. 2/3 = 8/12 and 1/4 = 3/12.
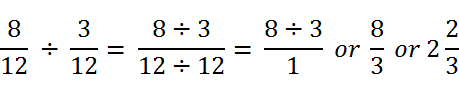In this equation, the quotient of the first expression gives us 1 in the denominator! So it effectively becomes 8 ÷ 3 or 8/3, which is 2 and 2/3. This technique just melts the fraction division away.
All of this happened in one class. And there were more problems than just this one and more voices than just mine. Students were explaining what they saw and why it made sense, and they were shouting “Eureka!” every time they understood something new. Many students were standing, and hands were waving all around the room. I can tell you that at times it got a little crazy. But this is how, at 12:20pm, after a long morning of classes culminating in a math lesson on the division of fractions, a group of 25 fifth-graders spontaneously erupted into applause. It certainly doesn’t happen every day.
Ours is definitely to wonder why.
Places and Bases
Recently in math class we have been working with decimals. This is one of the areas in math where a solid foundation in place value will take you a long way. If for instance you want to know the product of 15 and 3.2 it’s nice to know that 10 x 3.2 is simply a decimal move and 5 x 3.2 is just half again. I am always surprised to find that place value is not well understood by 5th grade. I guess I need to stop being surprised. But perhaps place value is just a little more complicated than we give it credit for, and maybe there is just not enough emphasis in the earlier grades.
Let’s look at the base-ten place value table:
| Thousands | Hundreds | Tens | Ones | Tenths | Hundredths |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 |
| 103 | 102 | 101 | 100 | 10-1 | 10-2 |
The reason for the ease of computations with 10 and powers of 10 is that ten is the base. This is why when you multiply 10 times anything “you just add a zero.” I try to teach my students to use the more mathematically accurate phrasing of “you just move the decimal,” but it’s no more challenging. The ones, or units, are the center of the place value system – all other places are exponentially larger or smaller than the base to the zero power.
Exponent review:
- All numbers to the zero power are equal to 1
- Negative exponents are just powers of base (ten in this case) in the denominator.
To understand place value, I find that it is helpful to examine what life is like in other bases. Let’s look at a base-five place value table like the one above.
| One hundred twenty-fives | Twenty-fives | Fives | Ones | Fifths | Twenty-fifths |
| 1000 | 100 | 10 | 1 | 1/10 | 1/100 |
| 53 | 52 | 51 | 50 | 5-1 | 5-2 |
In base 5 there is no numeral 6, or 5 for that matter. There are only 0, 1, 2, 3, and 4. Once you get to 5 the notation is 10 or more clearly written, 10five. The number 12ten is 22five, and the number 78ten is 303five.
When we want to multiply any number in base five times five all we have to do is move the decimal! 115 (which is 6 to us) times 105 (which is 5) is 110five (which is 30 to us). The product is still true regardless of the base. Likewise 22.2five (which is 12 and two-fifths) times 5 is 222five (12.4 * 5 = 62).
The place value system is dense, but when we understand the places and bases of our number system everything makes a whole lot more sense (or perhaps cents or pence if you live on the other side of the pond fence).
Division Story Problems
Students wrote some interesting division story problems today. We talked about making them real – though that can be tough – and we talked about making them meaningful – though that is certainly a challenge. I proposed to them that math should either be rather interesting or rather useful. Though story problems can fall into this category, they often don’t. For some senseless math check out what happens when we do stuff to numbers… because that’s what we do in math (not really). In the end they came up with a number of interesting and engaging problems that produced more to think about in their creation than in their solving. Here are a few:
There are 160 people at a party and there are 40 pies. Each pie is cut into 7 pieces. How many pieces would each person get?
Sasha made 117 cupcakes. She had platters that held 12 cupcakes each. How many platters does she need?
There are 157 students going on a field trip to Nisqually. There weren’t any buses, so they had to order “10 person” vans. One person brought their mom, dad, brother, and sister. Three teachers came as well. How many vans do they need to order?
The clock factory produces 20 clocks per hour. 143 clocks in the clock factory are finished. They are packed into creates that hold 44 clocks each. How many crates do they need? How many clocks are in the last crate? How long did it take to make the clocks in the first crate filled?
There were 260 3rd graders at a summer camp. Half of them were going to Great Wolf Lodge. A quarter of them were going swimming. The last quarter was staying at camp. The larger group took mini-buses that held 13 campers. The smaller groups took cars that held 5. How many buses and cars did they need?
I think some of these students could write for textbook companies! It’s interesting to see their worlds reflected in their math problems, and I was particularly happy to see how engaged they were in the process.